Solution to the Microsoft Interview Problem

Find the span between the columns if the distance between the lowest point and the ground is 20m, the height of the poles is 50m and the length of the string spanned between them is 80m

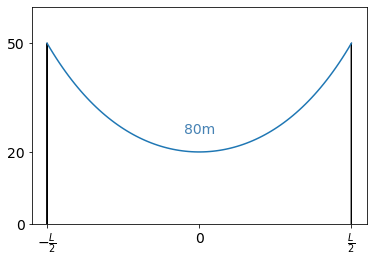
From the mechanics lessons, I remember that the chain spanned between two points under the gravitational force takes the shape of a \(cosh\) function. Hence, we are trying to solve \(f(x) = a cosh(b x)\), for \(a\) and \(b\). Here, I scale \(f(x)\) in such a way, that \(f(0)=1\) by dividing all measurements by 20.

Now, we have two unknowns that we want to find, hence we need 2 equations:

1) Let \(l = \frac{L}{2}\), then \(f(l) = cosh(a l)=2.5 \Rightarrow al = cosh^{-1}(2.5) \approx 1.5668\)

2) The length of a curve can be calculated by: \(l = \int^{l}_{0} ds = 2.5, \text{ where } ds = \sqrt{1 + \left( \frac{dy}{dx} \right)^2} dx\)

Now, we can use e.g. Numpy trapezoid numerical integration to calculate that integral. If we guess \(l\) (the half of the span between the columns), then parameter \(a=1.5668/l\).

def f(l):
    x = np.linspace(0, l, 1000)
    a = 1.5668/l
    
    return np.sqrt(1 + np.power(a*np.sinh(a*x), 2)), x

for l in np.linspace(1.15, 1.153, 100):
    if np.isclose(np.trapz(*f(l)), 2, atol=1e-10):
        print(l)

a = 1.5668/1.152
g = lambda x: np.cosh(a*x)

This simulation, gives us the answer to what the \(l\) could be. With \(l=1.15\) the integral integrates to 2.0, and after multiplying it by the scaling factor (20) we get \(l=23\) meters.

Answer:

The span between the poles is around 46 meters.